Research
研究
Summary of Research Accomplishments
これまでの研究業績の概要
私の研究対象は、まず第一に、「量子重力理論としての超弦理論であり、そしてその理解の試金石となる「ブラックホールの量子力学」である。
私は過去の研究の大部分を「量子重力理論」の研究に打ち込んできた。量子重力理論は難問中の難問であるが、そのブレイクスルーが「ゲージ重力対応」、(別名「ホログラフィー」)という、20年ほど前に超弦理論から生まれた概念である。これは後述の「私の研究目的」で詳しく説明する。量子重力理論を理解するために、私はこのゲージ重力対応という概念を最大限用い、量子重力の試金石ともいえる「ブラックホールの量子論」の研究に第一に打ち込んできた。しかし、私の研究はただ単にブラックホールの研究のみでは決してない。そのブラックホールの研究を通じて、実は様々な分野の物理学(物性物理、原子核物理、宇宙論、量子情報論)の研究にも同時に打ち込んできたのである。後述するように、ブラックホールの量子力学の研究は、「ゲージ重力対応」を通して、あらゆる分野の物理学に直結してくるのである。
ここでは私の研究業績を大きく2つのカテゴリーに分類して紹介する。一つは、過去の量子重力理論およびブラックホールの研究業績、もう一つはそのブラックホールの研究を通じた様々な理論物理学全般への応用研究の業績である。
Result 1
量子重力理論とブラックホールの研究業績
まず、私の過去のブラックホール研究の代表的な成果を以下列挙する。
※以下参考文献は、私の論文リストの論文番号に対応。
●漸近的平坦な時空中のブラックホール内部のisland(島)を世界で最初に発見
●量子ブラックホールの有効模型である飯塚 - Polchinskiモデルの提唱と情報回復/損失の解明
●ゲージ理論がどのような条件下でブラックホールと等価な系になりうるかの解明
●ブラックホールのホライズンとゲージ理論の対称性の回復の双対性の発見
●ブラックホールの外側の時空のゲージ理論での再現
●超対称性のないextremalブラックホールのアトラクター機構を世界で最初に発見
●3次元量子重力理論の厳密経路積分の計算を世界で最初に成功
●ゲージ理論のcomplexity(複雑性)を世界で最初に計算
●ブラックリング(ブラックホールのホライズンがドーナツ型)の微視的なエントロピーを世界で最初に導出

アインシュタインの一般相対論において、時空が極限まで曲がった例がブラックホールであり、ブラックホール内部の情報は、その極限重力のために古典的には決して外に出ることができない。1970年代にベッケンシュタインやホーキングらにより、このブラックホールの表面積という時空の幾何学量が、ブラックホールの「エントロピー」、すなわち「情報量」を表す量であり、ブラックホール自体、温度をもち熱力学に従ってふるまうことが明らかになった。同時に、ブラックホールは熱輻射し、やがて、消失されるため(ブラックホールの蒸発)、内部の情報が一見すると失われてしまい、量子論と矛盾するという点もホーキングによって指摘された。これがブラックホールの情報損失問題である。この議論では、ブラックホールを古典的な一般相対論で扱い、その時空上での曲がった時空の場の量子論を考慮している。
ブラックホールの蒸発が完全な熱輻射に基づいて行われるとすると、これはブラックホールでは量子力学の基礎原理が成立しない事を意味する(ブラックホールの情報損失問題)。私が過去に行ってきた研究は、一言で言うならば、「このホーキングによる、ブラックホールの情報損失問題をゲージ重力対応を通じて解明する研究」である。
ゲージ理論は量子論であるため、必ず量子力学の基礎原理に乗っ取っている。ゲージ重力対応によると、量子重力理論はゲージ理論と等価になる。故に、これは量子重力理論も必ず量子力学の基礎原理に乗っ取っている事を意味する。ここから、ゲージ重力対応は「情報は失われない」と予言する。しかし一方、ホーキングのブラックホールの熱輻射は、現代物理学の基礎である、「曲がった時空の場の量子論」という大きな指導原理に基づいている。故に、「情報は失われる」との予言も一見何も間違いがないように思える。私の過去の研究業績は、「このゲージ重力対応とホーキングの議論はどう整合性がつくのか?」「もしホーキングが間違っているのなら、ホーキングの計算の間違いは何か?」という根本的な問いに明確な回答を与えたという点にある。
漸近的平坦時空のブラックホール内部のisland(島)を世界で最初に発見
ホーキングによる、ブラックホールの情報が失われるという予言は、ゲージ重力対応の観点から考えると量子重力理論とゲージ理論の等価性から、明確に否定される。故にこのブラックホールの情報損失問題は、どのような量子重力効果を我々が見落としていたのか?という点に帰着する。2019年にこの分野で大きな発展があった。Penington(2019)らの仕事によると、ブラックホールの蒸発が進むと、ブラックホールの内部に、外部からその情報を「量子もつれ」を通じて完全に取り出せる領域(島:island)が発生し、その島(island)の結果、状態が量子力学の原理に基づいて時間発展するというのである。Peningtonによる本アイデアは説得力があるが、ゲージ重力対応を用いるなど非常に限られた状況下での議論であった。私はこのアイデアを、世界で初めて現実宇宙のブラックホールを表す漸近的平坦な時空に応用し、ゲージ重力対応の枠組みを超えて島(island)の概念が適用できることを示した業績[53], [52]がある。これはブラックホールの量子論の基礎となるユニタリー性が、ゲージ重力対応の適応できる漸近的Anti-de Sitter時空の重力理論のみに限らず、一般的な重力理論で成立するのか?という問いに、「成立する」という明快な答えを与える。
本業績は、ゲージ重力対応の枠組みにおさまらず、一般の重力理論でもブラックホールの蒸発が量子力学の原理に基づいて時間発展することを実際の解析を通じて世界で初めて示した重要な成果である。本論文2本は1年ほどでinspireでの引用数が2本とも50を超え、また雑誌quanta magazineによるインタビュー*1を受けるなど大きな反響を呼んだ。
[53] K. Hashimoto, N. Iizuka and Y. Matsuo,
"Islands in Schwarzschild black holes,"
JHEP 06, 085 (2020) doi:10.1007/JHEP06(2020)085 [arXiv:2004.05863 [hep-th]].
107 citations counted in INSPIRE as of 11 Nov 2022
[52] T. Anegawa and N. Iizuka,
"Notes on islands in asymptotically flat 2d dilaton black holes,"
JHEP 07, 036 (2020) doi:10.1007/JHEP07(2020)036 [arXiv:2004.01601 [hep-th]].
92 citations counted in INSPIRE as of 11 Nov 2022
*1 関連記事のURL:https://www.quantamagazine.org/the-most-famous-paradox-in-physics-nears-its-end-20201029
量子ブラックホール(via Gauge/Gravity対応)の有効模型である飯塚 - Polchinski モデル(IP model)およびその発展である飯塚 - 奥田 - Polchinskiモデル(IOP model)の提唱、およびゲージ理論がどのような条件下でブラックホールと等価な系になりうるかの解明
ブラックホールの蒸発が量子力学の基礎原理と矛盾する時間発展をするとホーキングが示した時、「時空に関しては古典近似」という仮定をしている。一方、量子重力は時空も量子論で取り扱う。故に次の問いに答えることは重要であろう。その問いは、「ゲージ重力対応に基づき、時空の古典近似に相当する極限を対応するゲージ理論でとると、ゲージ理論でも、一見、量子力学の原理に従っていないような非ユニタリーな情報損失現象が現れるか?」
本問いに対する答えが「イエス」であること、かつその情報損失を具体的に示すこと、および時空の古典近似をとらないならば、いかに情報が回復するか?これら全てを、私はゲージ重力対応の有効行列模型を新たに[15], [14]で提案し、全て具体的に示した。特に10次元時空に等価なゲージ理論を「トイモデル化」した研究[14]は「飯塚-Polchinski (IP) 模型」と呼ばれ、ゲージ理論がどのような条件下でブラックホールに等価な系になりうるかを明らかにした*2。これにより、ホーキングの議論に間違いは無いが、ただ彼の半古典近似が、一見量子論と矛盾する結果を与えているだけという点を明らかにした。本論文は引用数こそ60程度と少ないが、多くの超弦理論のリーダーたちの有名論文(Maldacena-Stanford 2016, Sekino-Susskind 2008、Gross-Rosenhaus 2016)などでも引用されており、https://arxiv.org/abs/1102.3566などのレビュー記事や、他にはMaldacenaの講演でも名前をつけて引用されており高い評価を受けている。
https://www.icts.res.in/sites/default/files/adscft20-2018-05-23-Juan-Maldacena-Lect2.pdf
[15] N. Iizuka, T. Okuda and J. Polchinski,
"Matrix Models for the Black Hole Information Paradox,"
JHEP 02, 073 (2010) doi:10.1007/JHEP02(2010)073 [arXiv:0808.0530 [hep-th]].
44 citations counted in INSPIRE as of 11 Nov 2022
[14] N. Iizuka and J. Polchinski,
"A Matrix Model for Black Hole Thermalization,"
JHEP 10, 028 (2008) doi:10.1088/1126-6708/2008/10/028 [arXiv:0801.3657 [hep-th]].
64 citations counted in INSPIRE as of 11 Nov 2022
*2 少しテクニカルに述べると、ゲージ重力対応は、ゲージ群SU(N)のNとニュートン定数GNがGN ∝ 1/N^2の関係だと主張する。半古典近似であるGN → 0の極限、すなわちNが無限の極限では、N^2のゲージ場が、文字通り無限の情報を蓄えることが可能になり、熱浴の役割をはたし、一方的に情報を吸い続けるブラックホールの「見かけ」の情報損失現象をあたえる。これをゲージ理論をトイモデル化した有効行列模型を作ってそのspectraが、模型のlarge Nの't Hooft coupling λの増加とともに、discreteからcontinuumに変化することを実際に示し、相関関数が指数関数で時間減衰することを具体的に示した。
ブラックホールのホライズンとゲージ理論の対称性の回復の双対性の発見およびブラックホールの外側の時空のゲージ理論での再現
IPモデルの論文のアイデアの原型となったのは、コロンビアでの大学院時代での私の最初の論文[1]で、そこでは重力対応を持つゲージ理論の有効理論から、ブラックホールのホライズン(表面)が、対応するゲージ理論ではどう理解できるか?について調べ、それがゲージ理論での「対称性の回復する点」に相当する事を解明し、そこからブラックホール内部自由度の記述を[3]で得ている。さらに、ブラックホールの外側のメトリックをゲージ理論から再現した成果(図3参照)もある。なおこれらの研究から得た結果により、如何に量子力学が重力の現象と関連するか、かつどのような時に重力双対が成立するかという研究へと人々が問いかけるようになったのである。
超対称性のないブラックホールのアトラクター機構を世界で最初に発見
超対称ブラックホールでは「アトラクター機構」という物理現象がおこる事が90年代に、Ferra-Kallosh-Strominger '95の仕事によって知られていた。この機構は、ブラックホールのホライズンで、理論のパラメータとなるスカラー場(モジュライ)の真空期待値が、特定の値しか必ずとらないという現象である(図4参照)。我々は[8]で、超対称性をもつブラックホールにのみ示すと考えられていたアトラクター機構が、超対称性がなくても温度ゼロのブラックホールであれば一般に成り立つ事を、世界で最初に我々が示した。この我々の論文をきっかけとして、温度ゼロで超対称性のないブラックホールの理解が劇的に進展した。本論文の引用回数は250を超える。
この現象は「ブラックホールの量子論的な理解」が背景にあるためである。その議論とは、「ブラックホールという非常に高エントロピーをもった(=高い縮退を保有している)物質のゼロ温度(=基底状態)での縮退度は、理論の保存電荷(チャージ)によってのみ決まると期待される。そのため、ブラックホールの縮退度であるエントロピーを与える、ブラックホールのホライズンも同様に理論の保存電荷(チャージ)によってのみ決まると期待される。したがって理論のパラメータとなるモジュライも、ブラックホールのホライズン上で自由な値をとれず、保存電荷(チャージ)のみで決まることが期待されるのである。また明らかなように、この議論は超対称性の有無に依存しない。」この議論こそまさに、ゲージ重力対応を利用し、重力側への新たな知見を、ゲージ理論から得た一つの具体例である。
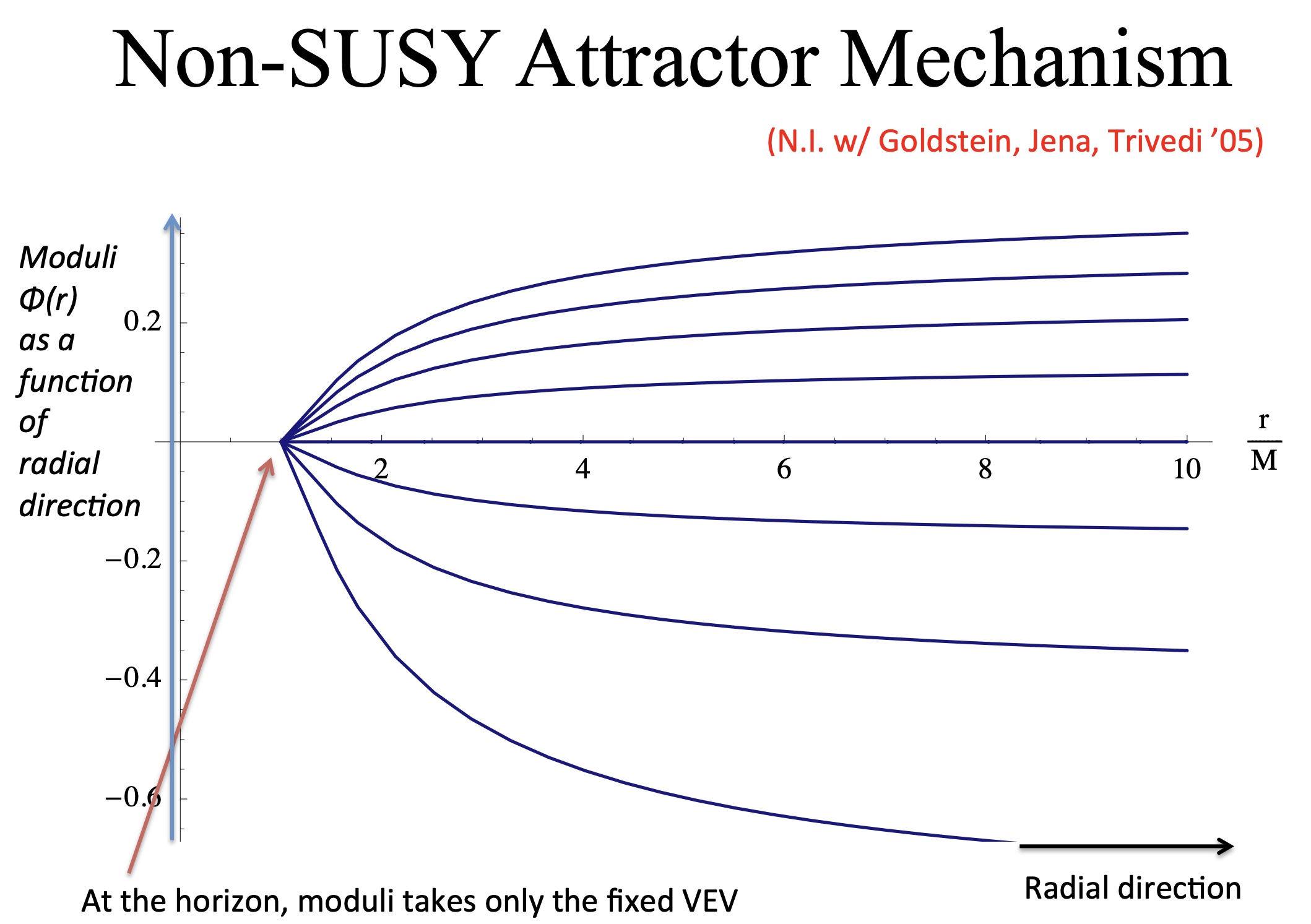
図4 超対称性のない温度ゼロブラックホールにおける新しいアトラクター機構の発見
ブラックホールホライズンでは質量ゼロの粒子の真空期待値がブラックホールの電荷のみで決定される
3次元量子重力理論の厳密計算を世界で最初に成功
3次元量子重力問題は4次元量子重力問題への試金石となる問題であるが、量子重力の経路積分を厳密に遂行した結果は出ていなかったが、我々は[42]でこの問題に挑戦した。我々は、3次元チャーンサイモンズ理論と3次元純粋重力理論が古典的には等価であることに着目し、かつ、この理論に補助場を導入し、超対称性化しても物理が不変であること、および量子論における経路積分を適宜定義することによって、3次元の量子重力の非摂動分配関数を、(近年超対称性理論で発展しているテクニックである)「局所化」という方法を用いて、世界で初めて厳密に計算し求めることに成功した。*3尚この仕事で、大阪大学でプレスリリースを行った。
リンク先URL:https://www.sci.osaka-u.ac.jp/ja/topics/4315/
*3 もう少しテクニカルに述べると、得られた分配関数は双対な2次元CFTの真空およびプライマリーとしてのブラックホールのキャラクターで表すことができ[44]、その係数からブラックホールの縮退(これは3次元ブラックホールのエントロピーと一致する)、およびその量子補正(これらはBekenstein-Hawkingエントロピーからの量子補正)と整合性がみてとれる。またこの結果を3次元でスピンが3以上の場を含む重力理論に拡張するとその結果は2次元CFTのWN対称性のキャラクターで同じように表せることをも示した[45]。
ゲージ理論のcomplexity(複雑性)を世界で最初に計算
ブラックホールとゲージ理論の熱平衡状態が対応するというのがゲージ重力対応から示唆される。一方、量子論的には、状態は熱平衡に達した後でも常に時間発展し続ける。この巨視的な物理量では測れない微細構造をよみとる物理量として、量子情報理論によるcomplexity(複雑性)が注目を浴びている。過去の研究ではこのcomplexity(複雑性)はスピン系でしか定義、計算されていなかったが、ゲージ重力対応の観点からはスピン系よりもゲージ理論で定義、計算されることこそ重要である。私は[48], [50]で、世界で初めてゲージ理論でこのcomplexity(複雑性)を定義し計算した。我々の研究をきっかけにゲージ理論の観点でcomplexity(複雑性)を理解する研究が大きく発展した。
[48] K. Hashimoto, N. Iizuka and S. Sugishita,
"Time evolution of complexity in Abelian gauge theories,"
Phys. Rev. D 96, no.12, 126001 (2017) doi:10.1103/PhysRevD.96.126001 [arXiv:1707.03840 [hep-th]].
94 citations counted in INSPIRE as of 11 Nov 2022
[50] K. Hashimoto, N. Iizuka and S. Sugishita,
"Thoughts on Holographic Complexity and its Basis-dependence,"
Phys. Rev. D 98, no.4, 046002 (2018) doi:10.1103/PhysRevD.98.046002 [arXiv:1805.04226 [hep-th]].
ブラックホールの微視的なエントロピーの導出:

超弦理論はアインシュタインの一般相対論を包括した理論であるが、より高エネルギー(=より短距離)で超弦理論と一般相対論の違いが重要になってくる。*4我々は[7]で、超弦理論の高次補正がホライズンの形成に重要な役割をはたす全く新しいタイプのブラックホール*5を発見し、そのホライズンの表面積からくるエントロピーを[9]で解析した。同時にそのブラックホールは、超弦理論により、微視的描像、つまり上述の状態数Wの数え上げてlogWを直接計算することも可能である。両者を業績[9](PRLで出版)で比較すると、ブラックホールの表面積によるエントロピーと、微視的な超弦理論のlogWの計算結果は、単なるベッケンシュタインとホーキングによる面積=エントロピーの関係式を超えて、高次補正までピタリと合うことを発見した(図5参照)。本研究はブラックホールのエントロピーの微視的な説明の成功という超弦理論の金字塔の具体例の一つである。
Black hole及びBlack ringのエントロピー計算
図5 ブラックホールのエントロピーの微視的計算
*4 例えば、Einstein Hilbert action に対して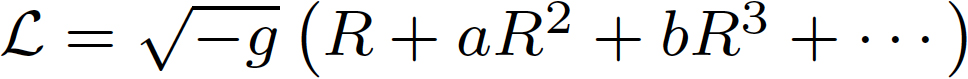 という補正が加わる。ここでa, b, c, · · · は超弦理論によって決まる特定の値である。
という補正が加わる。ここでa, b, c, · · · は超弦理論によって決まる特定の値である。
*5 よりテクニカルには、これはブラックホールの一種で、ホライズンの大きさが、弦の長さ程度で、ブラックリングと呼ばれる、ホライズンがドーナツの形をしたものである。
Result 2
様々な理論物理学全般への応用研究の業績
すでに述べたように私の研究の第一は量子重力理論であるが、あらゆる物理学全体に私は非常に興味をもち、物性物理への応用、ハドロン物理への応用、量子情報への応用、相対論への応用、宇宙論への応用といった様に、あらゆる分野との分野融合の研究をこれまでに成し遂げてきた。図6は、私が今まで執筆した論文のタイトルで使用したキーワードを並べたものである。これを見ていただければ私の研究が如何に弦理論、重力にとどまらず、物性論や原子核理論、量子情報理論などあらゆる分野にまたがり、非常に広大な物理学を研究対象としていることがわかっていただけると思う。しかしそれらは決して個々の研究としてやっているのでは決してない。量子重力/ゲージ重力対応という基点をもとに、自分の興味のおもむくまま仕事をしていたら、自然と多様な研究者をまきこむことになり、様々な物理学を含むことになった。私はそれこそが量子重力/ゲージ重力対応の研究なのだと思っている。なぜなら、ゲージ重力対応、およびブラックホールは様々な物理現象を理解する強力な「道具(ツール)」であるからである(図7参照)。
過去の私の論文のタイトルに含まれたキーワード

図6 過去の私の論文のタイトルに含まれたキーワードの一覧
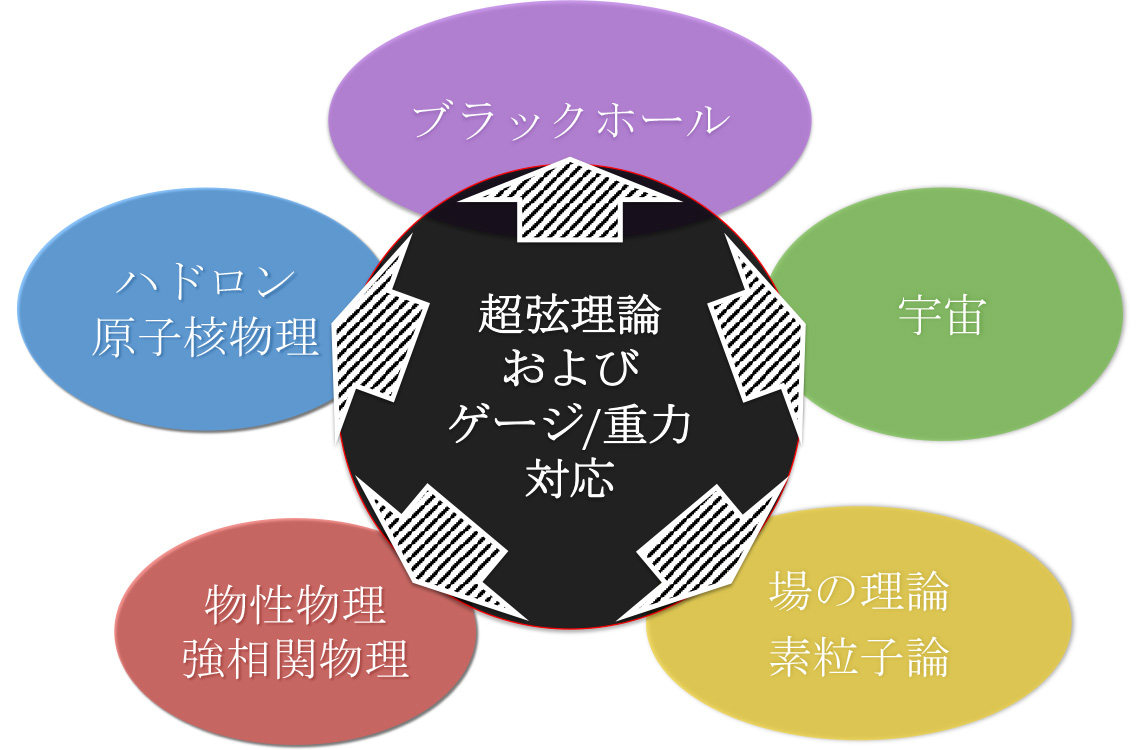
図7 ゲージ/重力対応は、超弦理論にとどまらず様々な物理現象を理解する強力な「道具(ツール)」である。
専門家の先生向けにもう一言だけ追加で述べさせていただきたい。ゲージ重力対応は「強結合の物理」が「弱い相互作用の弦理論、すなわち重力の理論」と対応している。(弱結合の)弦理論の最もシンプルかつエレガントな特徴は、それが唯一の整合性のある重力の量子論であるという点である。そして「ブラックホール」は、「重力の特徴がもっとも顕著に現れる物体」である。故に、「弱結合の弦理論のブラックホール」の研究は、ゲージ重力対応というレンズを介して見ると、それが「ゲージ理論の強結合現象がもっとも顕著に現れる物体の研究」に自然と結びついているということを納得していただけるのではないかと思う。まさにこれこそが、私の研究のもう一つの柱である、様々な理論物理学全般への応用研究の根幹なのである。そこには、「ブラックホール研究は、強結合の物理学の研究そのものである」という私の信念がある。
ここではそれぞれの分野への応用の仕事の代表例についてまず列挙する。
●場の量子論への架け橋:場の理論のエネルギーテンソルTµν の整合性条件の発見(CANECの発見)
●原子核理論への架け橋:原子核核力の計算と中心斥力の存在証明
●物性理論への架け橋1:非フェルミ流体の存在判別式の発見
●物性理論への架け橋2:一様だが、単純な並進対称性をもたない強結合場の量子論の真空の分類
●物性理論への架け橋3:永久電流に双対な重力解の世界で最初の発見およびLandau-Tiszaの超流動二流体モデルの関係式
●宇宙論への架け橋:フラックスコンパクト化とmoduli問題を解決した超弦理論インフレーション
そして以下これらについて手短に解説する。
場の量子論への架け橋:場の理論のエネルギーテンソルTμνの整合性条件の発見(CANECの発見)
どのような場の理論が理論として整合性をもつかは非常に重要な問題である。これをエネルギーの観点から考えると、どのようなエネルギーテンソルTμνが整合性をもつか?という問いになる。特にエネルギーはCasimir energyなどが負の値を持ち得る点に注目すると、いかに摂動近似を用いずに、この問いに対する答えを得るかは、場の量子論を深く理解する上で非常に重要な問題である。
本問題に対し、私は[51], [54]で、重力双対を持つ場の理論がどの様なエネルギー条件を満たさなければいけないかを、ゲージ重力対応を利用し、対応する重力理論の時空の因果律から制限を与えた。その結果、ストレステンソルのnull方向の積分値は必ず正でなければならない、すなわちCANEC(=conformally invariant averaged null energy condition) を満たしていなければいけないことが我々によって発見された。本研究は双対な時空の因果律という一般相対論の観点から、世界で初めて、一般的な曲がった時空の場の量子論のエネルギー条件を、非摂動で与えた重要な成果である。そういう意味では、これは重力と一般相対論との架け橋となる業績とも言える。
[51] N. Iizuka, A. Ishibashi and K. Maeda,
"Conformally invariant averaged null energy condition from AdS/CFT,"
JHEP 03, 161 (2020) doi:10.1007/JHEP03(2020)161 [arXiv:1911.02654 [hep-th]].
[54] N. Iizuka, A. Ishibashi and K. Maeda,
"The averaged null energy conditions in even dimensional curved spacetimes from AdS/CFT duality, "
JHEP 10, 106 (2020) doi:10.1007/JHEP10(2020)106 [arXiv:2008.07942 [hep-th]].
原子核理論への架け橋:原子核核力の計算と中心斥力の存在証明
ゲージ重力対応は強結合のlarge N SU(N)量子色力学と量子重力の等価予想であるため、ここのクォークを導入するとlarge N QCDを重力で解析できる。特にlarge N QCD(クォークやグルーオンを記述するゲージ場の理論)を解析しようとする試みはHolographic QCD と呼ばれ、私は過去、原子核物理学への応用の研究を行ってきた。過去の代表的な研究成果としては、任意の数のバリオンのダイナミクスを記述する、全く新しい行列理論(核力行列模型)を、超弦理論の枠組みで、ゲージ重力対応を用いて第一原理的に導出した業績[18]がある。その我々の核子行列模型から、核子のスペクトラムや、2体核力の導出のみならず、[19]で3体力をも導出する事に成功した。これは、QCDのような「クォークの閉じ込め」を強結合下で起こすlarge Nゲージ理論で、超弦理論の知識を駆使し、核力を“第一原理”から計算した画期的な仕事である。また我々の核子行列模形から、近距離2体核力はかならず中心斥力をもつ事を、一般的に示せる[18](図8参照)。本研究はまさに超弦理論から核力の導出というゲージ重力対応の醍醐味が現れた例である。
"String theory derivation" of the short-distance nuclear force

図8 large N QCDの原子核の核力の存在を、超弦理論の“第一原理計算”で示す
物性理論への架け橋1:非フェルミ流体の存在判別式の発見
高温超伝導で現れる量子臨界点では、準粒子近似が破綻し、非フェルミ流体がダイナミクスを支配している。この量子臨界点について様々な研究がなされているが、その解析は一般に難しく、その理由は、その臨界点が、場の量子論の強い相互作用特有現象だからである。一方、ゲージ重力対応は重力理論と強く相互作用する場の量子論の等価予想なので、ゲージ重力対応を利用して、重力/ブラックホールの解析から、強く相互作用する場の量子論の物理を探るのは自然なアプローチである。私にはこのゲージ重力対応を利用し、様々な強結合の場の理論の相転移や物性の輸送現象に関する研究を、ブラックホールの解析を通して行ってきた業績がある。
特に、代表的なものの一つに[23]がある。ここでは、ゲージ重力対応が成立する場の量子論の低エネルギー(ゼロ温度)極限で、いつ準粒子近似が破綻し、どのような非フェルミ流体が発生するかについて、系統的に調べた。その結果わかったことは、ゲージ重力対応が成立している場の量子論という特別な場の理論であれば、真空の対称性だけできまるたった二つのパラメーターの和の値の大きさで、非フェルミ流体の有無が判別できるという驚くべきものである[23]。本研究は高い評価を受け、引用数も180を超え、さまざまな場所で講演を行った。これは如何にゲージ重力対応/量子重力理論とブラックホールの解析が、非自明な場の量子論の物理を出してくるかという非常に面白い一例である。またラッティンジャーの定理がゲージ重力対応を用いて、非フェルミ流体の存在によりいかに破れるかについて解明した業績[26]もある。
物性理論への架け橋2:一様だが、単純な並進対称性をもたない強結合場の量子論の真空の分類
また[24], [30]では、強結合の場の量子論の真空が、空間的に一様ではあるが、必ずしも並進対称性を持たない、非等方な場合について、対応する重力解(より正確にはブラックホールのホライズン)をBianchi型のclassification *6を用いて完全分類した。このような一様並進対称性を仮定しない、時空および場の量子論の真空の分類は、我々の仕事が世界初であり、教科書などでも大きく紹介されており、(例えば、物性理論の先生らによる比較的新しい教科書:Zaanen-Liu-Sun-Schalm *7, "Holographic Duality in Condensed Matter Physics"の12章:Breakingtranslational invarianceは我々の仕事およびそれに基づく発展を中心に記述されている。)また高温超伝導で現れる「非対称な真空」は我々の重力側での記述のタイプVII型に相当する。
[24] N. Iizuka, S. Kachru, N. Kundu, P. Narayan, N. Sircar and S. P. Trivedi,
"Bianchi Attractors: A Classification of Extremal Black Brane Geometries,"
JHEP 07, 193 (2012) doi:10.1007/JHEP07(2012)193 [arXiv:1201.4861 [hep-th]].
86 citations counted in INSPIRE as of 11 Nov 2022
[30] N. Iizuka, S. Kachru, N. Kundu, P. Narayan, N. Sircar, S. P. Trivedi and H. Wang,
"Extremal Horizons with Reduced Symmetry: Hyperscaling Violation, Stripes, and a Classification for the Homogeneous Case,"
JHEP 03, 126 (2013) doi:10.1007/JHEP03(2013)126 [arXiv:1212.1948 [hep-th]].
63 citations counted in INSPIRE as of 11 Nov 2022
*6 例えばランダウリフシッツ:「場の古典論」
物性理論への架け橋3:永久電流に双対な重力解の世界で最初の発見およびLandau-Tiszaの超流動二流体モデルの関係式
先の並進対称性を持たない時空の分類の仕事と関連して、並進対称性が破れた超伝導状態状態における永久電流に双対な重力解を世界で初めて発見した業績[37](PRL で出版)がある。本研究は非常に面白い。外場/外力がない状態で永久電流が流れている超伝導に双対な時空を、我々は非常に複雑なEinstein方程式を解いて得たのであるが、その解の示唆する意味をゲージ重力対応を通じて考えると、およそ80年ほど前に発見されたLandauとTiszaによる超流動二流体モデルの関係式が導かれる *8!
このように、物性理論への応用は、ゲージ重力対応のなかでも一際私が興味をもって取り組んできたテーマであり、現在も非常に面白い論文を執筆中であり、並々ならぬ興味をもって研究を行なっている。
*8 SonnerとWithersも我々とは独立にこの公式を重力側から発見している。
宇宙論への架け橋:フラックスコンパクト化とmoduli問題を解決した超弦理論インフレーション
超弦理論は10次元の理論なので、6次元をコンパクト化しなければ4次元の物理がでてこない。しかし安直にCalabi-Yau空間に6次元をコンパクト化してしまうとさまざまな質量ゼロのmoduliがでてきてしまう。無論現実にはこのようなmoduliは観測されていない上、こういうものが存在していると初期宇宙のビッグバン元素合成などの標準宇宙論の概念と大いに矛盾する。故にこのようなmoduliは質量を獲得しなければならないわけだが、この質量をフラックスコンパクト化によってあたえると、初期宇宙にあったであろうインフレーションを引き起こす‘インフラトン’の質量も相互作用によって一般に与えてしまうことになる。研究[6]ではこの問題をいかに避けるか、そしてどのようなコンパクト化でインフラトンのみ質量を与えることなく、同時にmoduli問題を回避するかについて議論し、両者を解決する超弦理論の枠組みでは世界で最初の成功モデル *9を与えた。本論文のinspireでの引用数は100を超える。これも超弦理論から宇宙論の架け橋となる業績である。
*9 このモデルで重要なポイントはCalabi-Yau空間内に局在した2つのブラックホールである。本論文のポイントは、この2つのブラックホールの中心ではインフレーションに必要なフラットな方向を持ち得るという点にある
このように、私は物理学全般という非常に広い領域に興味をもち、それらにゲージ重力対応を応用し、様々な分野のトップ物理学者と共同研究/議論を重ねてきた実績がある。繰り返しになるが、これらのことはダイバースに単にいろいろやっているのでは決してなく、量子重力/ブラックホールという基点をもとに研究を行なってきた結果、自然と多様な物理学を含むことになったのである。まさにこのことこそが量子重力の研究であり、先に述べた、「弱結合の弦理論のブラックホール」の研究が「ゲージ理論の強結合現象がもっとも顕著に現れる物体の研究」に結びついているという根本的な信念がある。そしてこれらの研究の先は、次の着任後の研究計画で記述するように、単なるゲージ重力対応の応用ではなく、そのゲージ重力対応という様々な物理を理解するツール自体の開発であり、それを通じた極限状態の宇宙の理解なのである。